I receive new postings from SearchFunder in my Inbox. BVR calculates MVIC:EBITDA ratios from transactions. The headline reads: Industry Summaries > Miscellaneous Manufacturing (NAICS: 339). BVR publishes ratios (from two quantities, i.e., MVIC and EBITDA) along with corresponding percentiles. For example, the sample statistics are, as follows: (3.83, 25th percentile); (6.96, 50th percentile); (14.74, 75th percentile); and transaction sample size, 504, over a period of time. That's it? -- Where's the distribution? The sample size is mostly irrelevant for this calculation as only about six independent values would be necessary for robust sample statistics. Nonetheless, there is enough sample statistics to define a probability distribution. We could, then, generate random values from a specified distribution based on three statistics. The aim is to evaluate our decisions under more predictable outcomes. I've inserted the results of the MetaLog [See Note 1] to visualize the distribution, a complete picture of probabilities for a proxy on exit multiples.



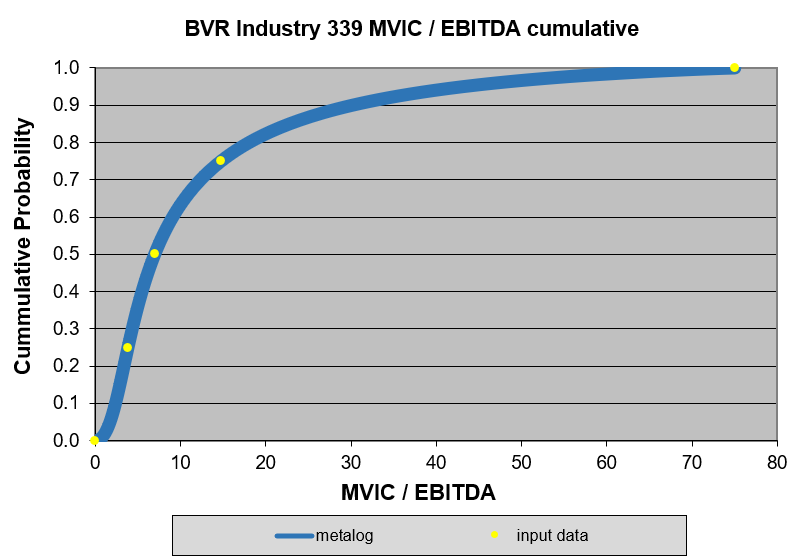
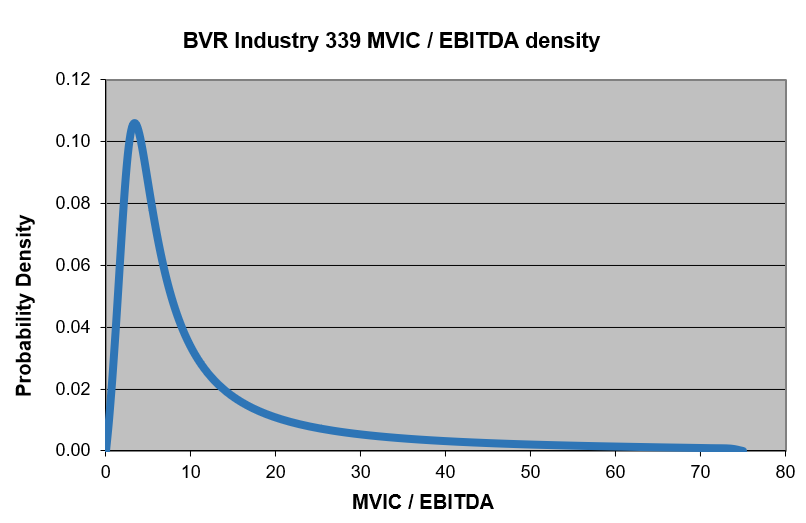
The distribution shows the process from which the fitted values are generated. The min. and max. values are the assumed bounds of the distribution (to avoid any discontinuities along the curve).


Note 1: "In economics, business, engineering, science and other fields, continuous uncertainties frequently arise that are not easily 0r well-characterized by previously named continuous probability distributions. Frequently, there are data available from measurements, assessments, derivations, simulations or other sources that characterize the range of uncertainties. But the underlying processes that generated this data are either unknown or fail to lend itself to convenient derivation of equations that appropriately characterize the probability density (PDF), cumulative (CDF) or quantile (inverse CDF) distribution functions. Introduced in 2016, the Metalog distributions are a family of continuous probability distributions that directly address this need." -- http://www.metalogdistributions.com/home.html